熵变什么意思（熵变的意义）

100次浏览发布时间：2024-11-09 09:18:53

在热力学中，熵是平衡态热力学的一个态函数，它的定义为：

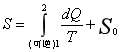
其中，1和2是两个平衡态，积分路径沿着任意可逆过程，T为热源温度，dQ是某一微小过程中系统吸收的热量，这样定义的物理熵有以下几方面的意义。

1 熵增原理是热力学第二定律的数学表达式

系统由一种状态到另一种状态，在此过程中，必然伴随着熵值的改变。在热力学理论中，人们所指的熵变一般是指熵增加。我们知道，可逆过程发生后，所产生的后果可以完全消除而令一切恢复原状；而不可逆过程发生后，则用任何曲折复杂的方法都不可能令一切恢复原状。这一事实说明，过程是否可逆实际上是由初态和终态的相互关系决定的。而熵函数在初态和终态的数值可以用来判断过程是否可逆或不可逆，判断不可逆过程的自发方向，熵增加原理可以对过程的性质及方向进行判断。

熵增加原理：任何物理过程中各个参与者的总熵必定是要么增加，要么保持不变，熵不会减少，即

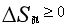
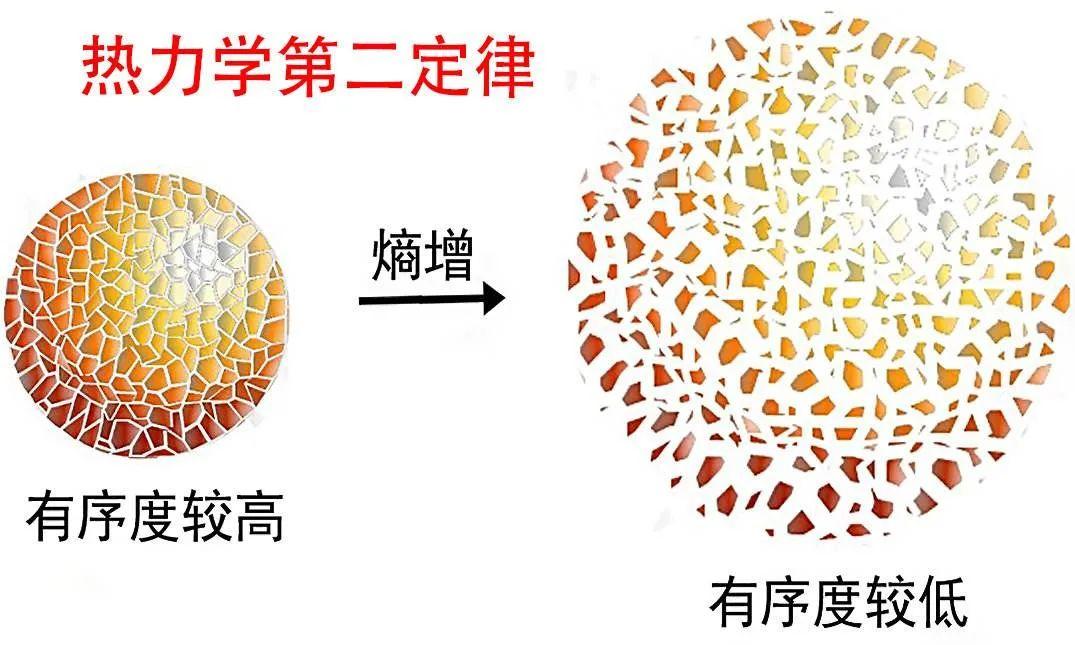
熵增加原理实际上预言了大多数过程是不可逆的——不能向相反方向进行，过程必定朝熵增加而不是熵减少的方向进行。这一原理告诉我们，在没有外界干预的条件下，系统自发地由有序趋于无序，最后达到热平衡。换言之，熵值越低，有序程度越大。随着熵增加，有序程度越来越低，最后完全变成无序状态。过去人们认为，对一个生物系统而言，熵增加原理应该自发地由有序变为无序，最后达到平衡态，也就是死亡。而生物进化论告诉我们，生物是进化的，可以由简单到复杂，有序程度可以越来越高。熵增加原理的应用是有条件的、有限的。

2 熵在微观上表征系统内粒子的混乱程度

在统计物理中，由玻尔统计理论或量子统计理论都有如下关系式：

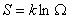
这就是著名的玻尔兹曼关系式。k是玻尔兹曼常数，Ω是系统的微观状态数。在宏观条件不变的情况下，系统具有大量的微观状态。当系统处于平衡时，微观态数越多，系统越混“乱”，熵就越大；否则，熵就越小。从微观意义上讲，熵是物质系统无序性和混乱度的量度。

平衡态体系内微观粒子无规则运动与非平衡态粒子运动相比混乱度更大，即当粒子无规则运动最乱、最无序时，才能使体系内部各处的温度、密度等性质达到均匀一致，以致最后趋向于平衡态，所以熵增加的过程，即孤立系统由非平衡态趋向平衡态的过程，正是体系内微观粒子无规则运动由不太乱变得更加乱的过程。由此可见，熵的物理意义在微观上正是粒子无规则运动混乱程度（或无序程度）的量度，熵增加就是从有序向无序发展的过程。

3 熵在宏观上表征能量分布的均匀程度

能量都是由于从非均匀分布倾向于均匀分布的过程中转化做功的，即要能量成为可利用能，即将能量用于作功，必须在一定的空间中造成能量密度的差异，使能量从高密度区流向低密度区，就可以获得功。能量分布越不均匀，有序度越高，则熵就越小，能量转化为功的效率越高。若能量分布已完全均匀，熵达到最大，这时不可能再发生能量从这一区转到另一区的宏观流，也就不能获得功。熵增加在宏观上，表征不可利用能的增加，即意味着有效能量的减小，时间永远向前运动，能量只能沿有效状态转化为无效状态的耗散方向转化。因此，我们说热力学第二定律（即熵增原理）是能量转化的“质”的定律，熵是时光之箭。